中山大学物理学院、本实验室阴帅副教授团队与中国科学院物理研究所李自翔特聘研究员团队合作,近期在费米子符号问题研究中取得新进展。他们提出一种基于非平衡虚短时量子临界动力学以有效规避费米子符号问题进而准确确定量子多体系统的基态相图与临界性质的新方案(如图1)。依托这一方法,团队首次揭示SU (3)狄拉克费米子Hubbard模型的基态相图及其量子临界性,发现一类非常规的Chiral SU(3)普适类。
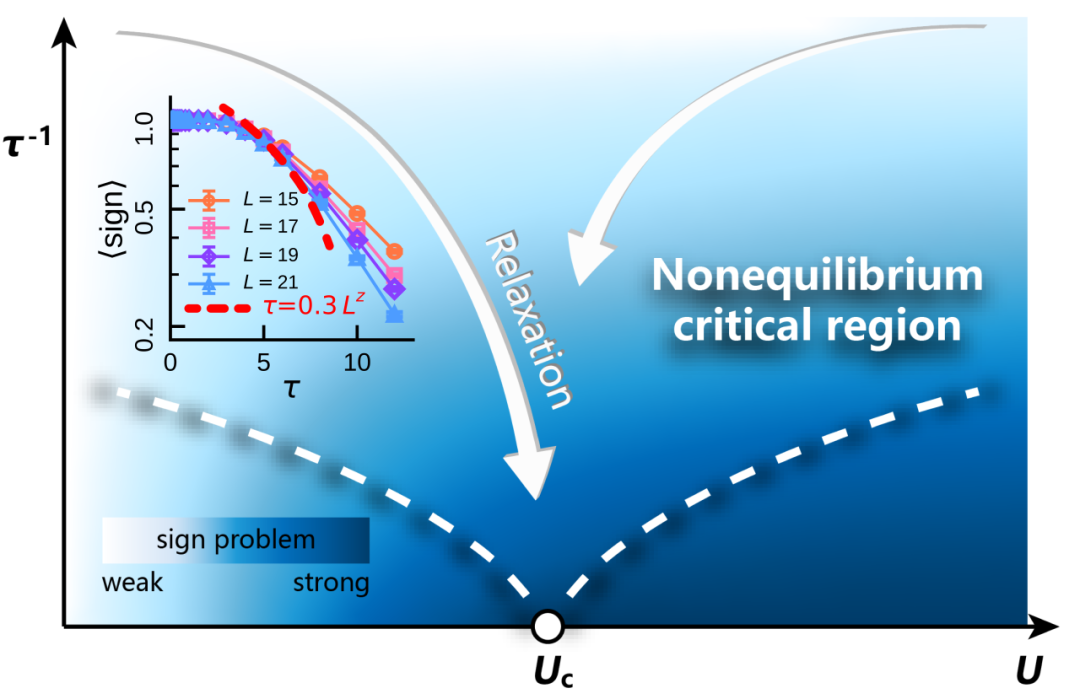
图1 通过虚短时量子临界动力学规避符号问题并探测量子临界性
作为量子蒙特卡洛方法的核心障碍,符号问题极大制约了关联量子体系的数值探索。其根源在于费米子的交换反对称特性,使得蒙特卡洛模拟中产生负概率难题,无法实现高效的重要性采样。在传统量子蒙特卡洛对关联体系量子相变的研究中,通常需先通过虚时间演化让系统达到基态,再计算物理量的临界性质,而符号问题会随虚时间演化显著加剧,导致基态难以准确确定。
针对这一困境,研究团队突破 “先确定基态再分析临界性质” 的传统思路,转而聚焦虚时弛豫动力学的非平衡短时阶段,利用系统短时阶段的标度行为确定基态量子临界性质,为有符号问题模型的量子临界性的研究提供了新路径。
在经典相变中,短时临界动力学最初由H. K. Janssen等提出,并广泛用于确定经典相变临界性质。在量子相变中,阴帅,麦培智和钟凡教授发展出虚短时量子临界动力学标度理论。中国科学院物理研究所张士欣特聘研究员和阴帅首次在量子计算机平台实验验证了该理论。
在本研究中,团队发现对于一些存在符号问题的强关联系统,若从符号问题较弱或无符号问题的初态出发,在系统虚时演化的短时阶段,符号问题仍处于可控范围,且系统演化行为可通过虚短时量子临界动力学标度理论刻画。由此,可利用虚短时量子临界动力学标度理论可靠提取系统的基态相图与临界性质。
研究团队聚焦SU(N)狄拉克费米子Hubbard模型。当N为偶数时,该模型无符号问题,已有大量研究揭示了其丰富的相图和临界性质。当N为奇数时,该模型有符号问题,其相图和相变性质仍未知。基于虚短时临界动力学方案,研究团队成功揭示SU(3)狄拉克费米子Hubbard模型的基态相图,发现了该模型的有序相存在一类新的λ8-反铁磁序(如图2)。此外,该研究还进一步揭示了狄拉克半金属相与λ8-反铁磁序之间的量子相变的临界性质,并发现这个量子临界点属于新的Chiral SU(3)普适类,超越传统狄拉克费米子临界性的Gross-Neveu理论。
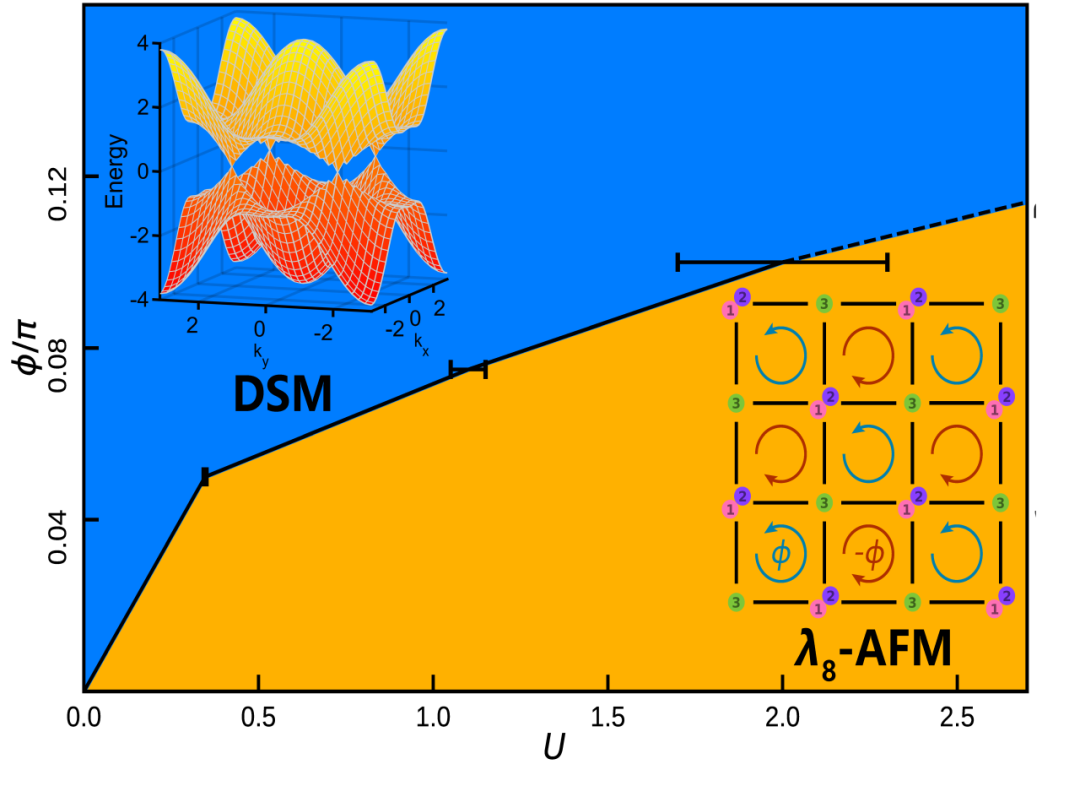
图2 通过虚短时量子临界动力学确定的SU(3)狄拉克费米子Hubbard模型相图
该成果以 “Preempting fermion sign problem: Unveiling quantum criticality through nonequilibrium dynamics in imaginary time” 为题,于2026 年1月1日发表于国际权威期刊《科学・进展》(Science Advances)。中山大学物理学院本科生余荫铠(现中国科学院物理研究所研究生)为论文第一作者;中山大学物理学院、本实验室阴帅副教授与中国科学院物理研究所李自翔特聘研究员为共同通讯作者;中山大学研究生黎智轩参与了相关研究。研究得到国家自然科学基金、广东省及广州市科技计划项目的支持。









