
在现代数字通信系统的核心评估体系中,EVM(Error Vector Magnitude,误差向量幅度)是一项至关重要的性能指标。几乎在所有现行的通信标准中,都明确规定了EVM的衡量标准,并且这一指标还在随着通信协议的不断演进而持续发展。
举例来说,5G NR蜂窝系统和Wi-Fi7系统对发射通路EVM的要求如下表所示。EVM在两种系统中都占据着重要位置,尤其是在Wi-Fi通信系统中,EVM甚至可能被视为Wi-Fi系统射频性能评估中的首要指标。
被广泛使用的EVM究竟代表什么物理含义?为什么对于现代通信系统如此重要?为什么EVM有%和dB两种表示单位?EVM指标又是如何计算及如何使用的?
我们带着这些问题,试着重新详细认识“EVM”这一既常见又略显神秘的重要性能指标。
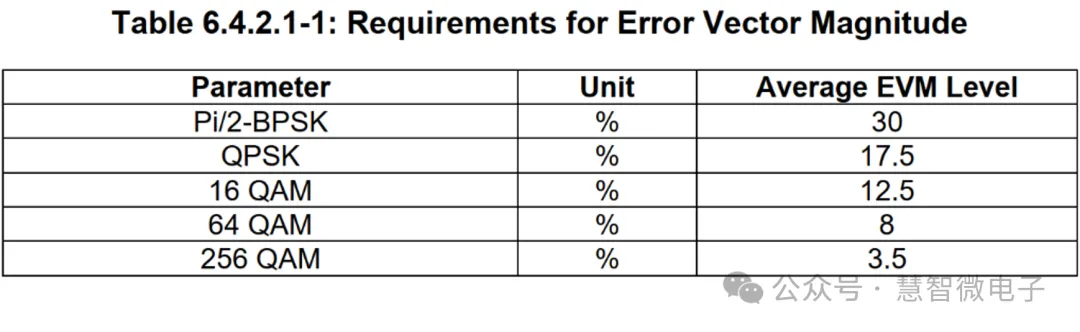
图:5G NR发射通路的EVM要求
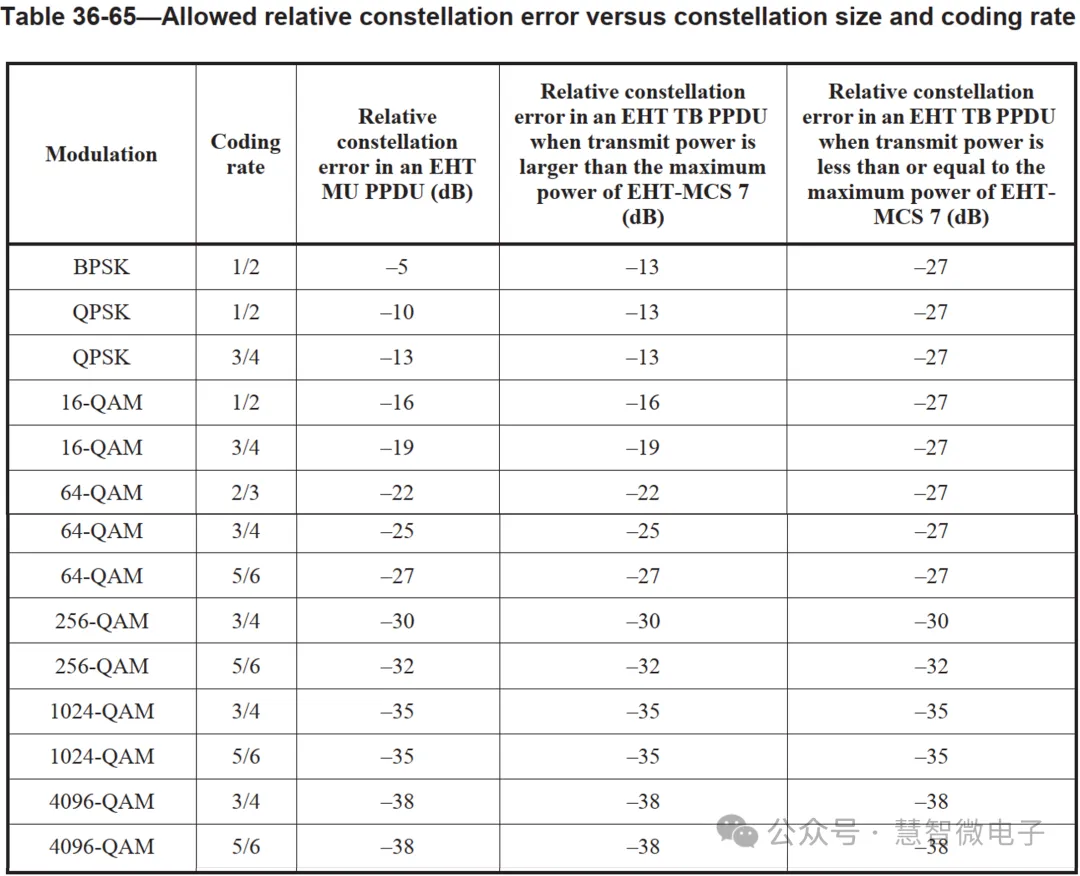
图:Wi-Fi7发射通路对星座误差(EVM)的要求
EVM的来源
左手数字,右手模拟:重要的数字调制技术
在通信的早期时代,模拟通信系统占据主导地位。信号作为模拟量,在幅度、频率上进行转换及传输。然而,模拟信号抗干扰能力差、保密性差、传输距离受限,且难以支撑复杂的通信系统。于是,在20世纪80年代,随着数字通信技术和集成电路技术的迅猛发展,通信技术逐渐从模拟向数字转型。

图:模拟通信技术向数字通信技术的转换
在这一转型过程中,数字调制技术成为了关键。
在数字通信中,尽管信号处理已经数字化,但数字“0”和“1”无法直接漂浮在空中,因为自然界中传输的仍然是具有特定物理量值的模拟信号,转换后的数字信号仍需以某种形式映射到模拟信号上。而实现数字信息和模拟信号传输桥梁和映射的,正是数字调制技术。
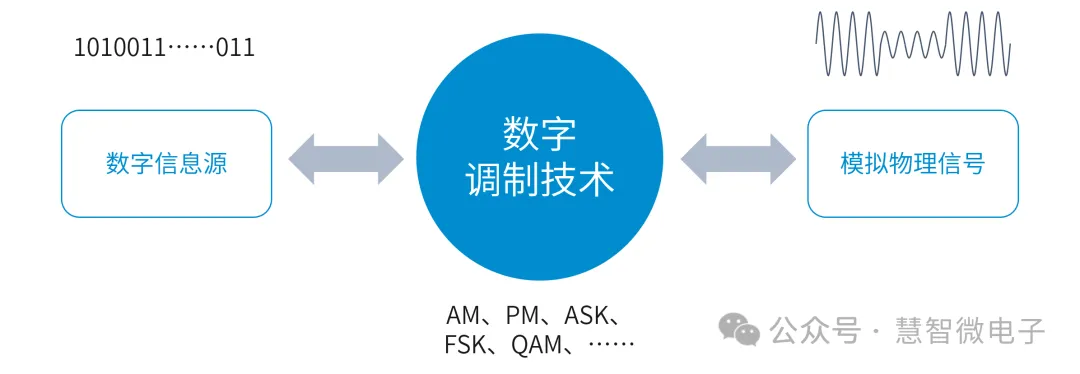
图:数字调制技术完成的功能
常见的数字调制技术包括ASK(Amplitude Shift Keying,幅度键控)、FSK(Frequency Shift Keying,频移键控)、QAM(Quadrature Amplitude Modulation,正交幅度调制)等。这些技术通过特定约定,建立起数字信号与模拟信号的对应关系,然后通过改变模拟信号的不同参数来传递数字信息。
以16QAM举例。16QAM信号数字信息和模拟信号的对应可以由星座图直观反应出来。下图为16QAM调制下信号的星座图表示。
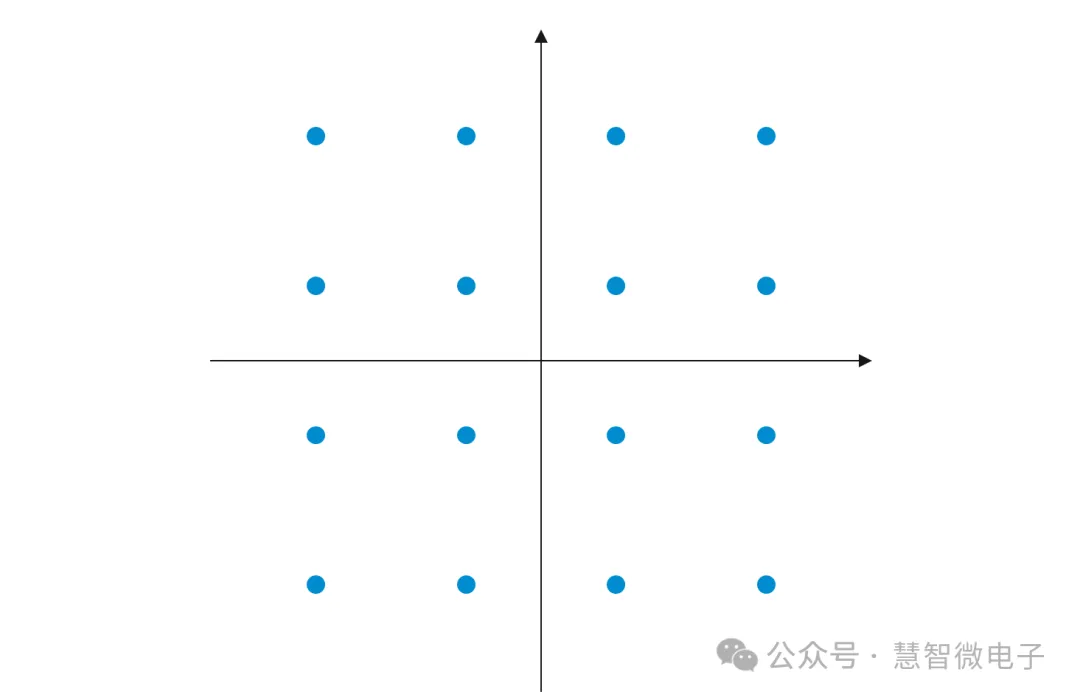
图:16QAM信号的星座图表示
在16QAM的星座图中,一共有16个点,所以可以代表16个不同的数字信息。每个点,就称为一个符号(Symbol)位。在2进制中,16可以由2的4次方来表示。所以16QAM中的每一个点,可以代表4位不同的2进制信息。也就是常说的,16QAM中的每个符号代表4个bit的信息。
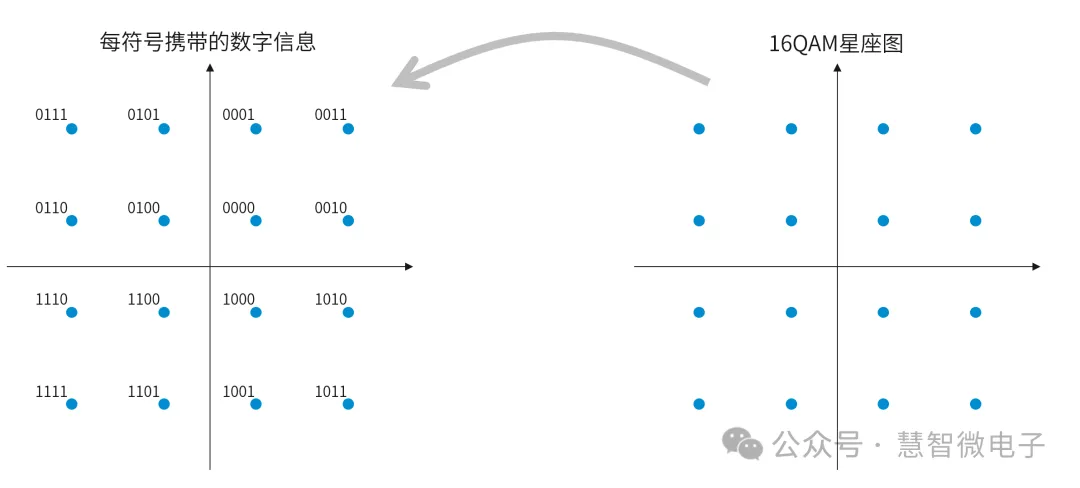
图:左手数字:16QAM中每个符号携带4个bit数字信息
在星座图上,也可以显示出来每个符号所对应的模拟信息。比如对于位于A位置的信号,其幅度就为a,相位就为α。对于位于B位置的信号,其幅度就为b,相位就为β。有了幅度和相位,就可以相应得出来唯一确定的模拟信号。
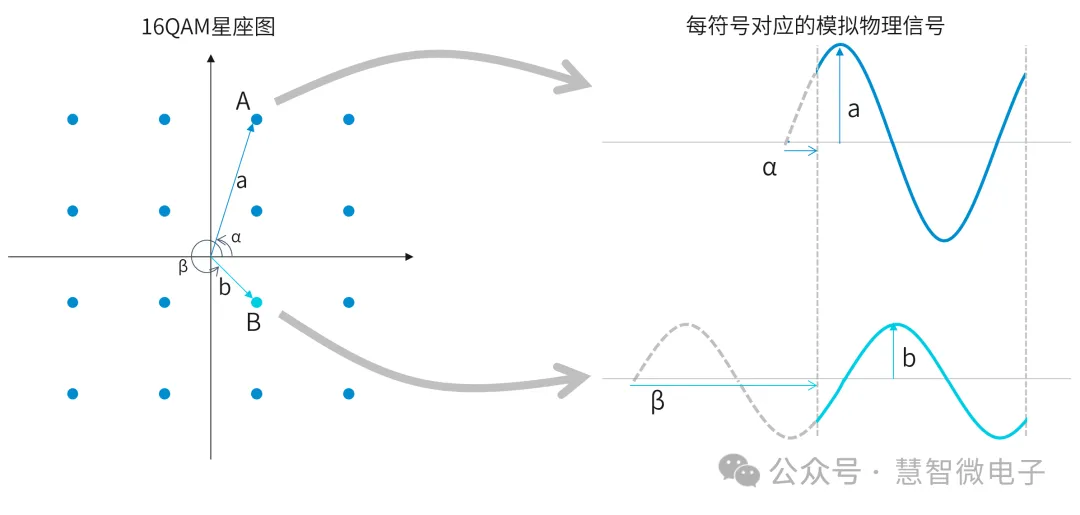
图:右手模拟:16QAM中的符号与模拟物理信号的对应
在数字信号的调制中,每一个符号都建立起数字和模拟的严格对应关系。左手数字,右手模拟,通过数字信号调制技术,数字世界和模拟世界就此连接。

图:数字信号调制技术将模拟世界和数字世界相连
EVM:数字信号调制效果的裁判
在数字信号调制中,每个符号的所在位置都非常重要。虽然数字通信有较强的抗干扰能力,符号位置发生轻微偏移并不影响通信。但如果偏移位置较多,就可能造成信号传输的误码,造成信号传输的错误。
如何来衡量数字信号调制的实际效果是好还是坏呢?这时就引入了误差向量(Error Vector)指标。误差向量反应实际信号和理想信号之间的差别。
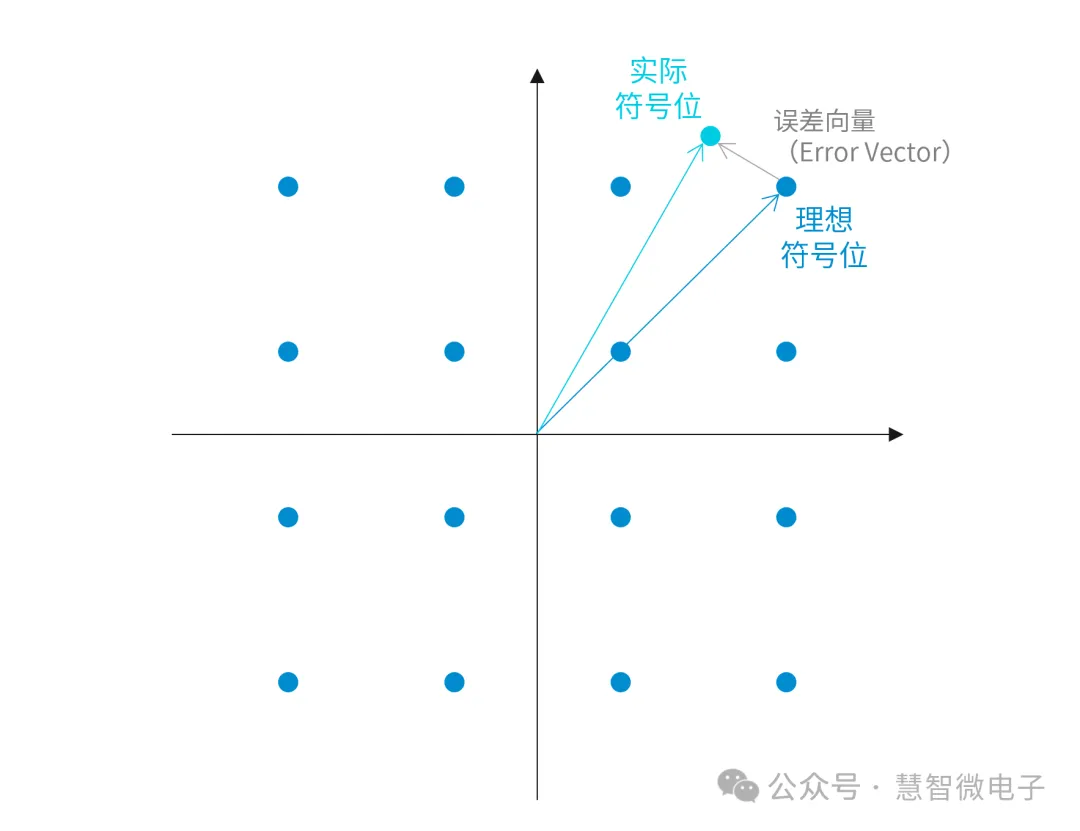
图:误差向量的引入
EVM的定义
在星座图中,任何一个符号都有其对应的理想位置,也即有确定的幅度及相位。但在实际信号中,总是会存在误差。
误差主要分为两种,分别是幅度误差(Magnitude Error),以及相位误差(Phase Error)。幅度误差反应信号幅值的大与小,相位误差反应信号的超前与滞后。
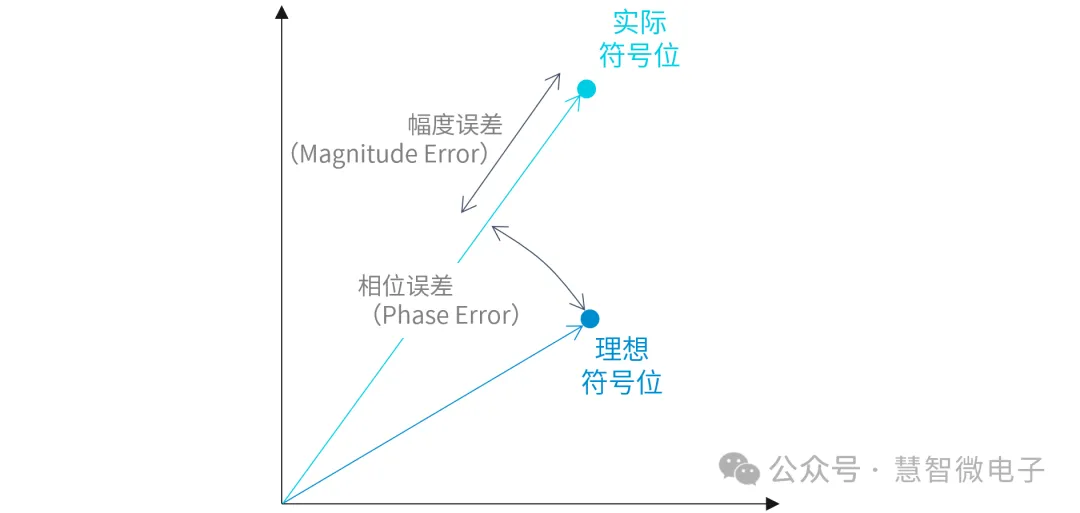
图:实际信号与理想符号之间的误差
在实际应用,可以用一个连接理想信号和实际信号的向量,把幅度误差和相位误差统一表示出来。这个向量就叫“误差向量(Error Vector)”。
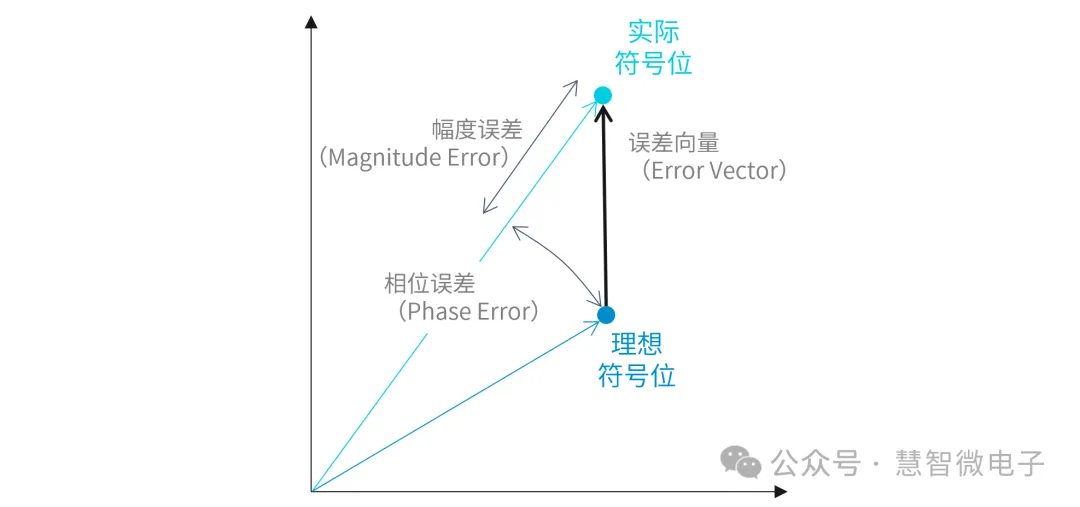
图:误差向量(Error Vector)
在实际应用中,实际信号和理想信号之间的距离更能反应信号质量的好坏,而不是两个信号之间的角度差。所以会单独把误差向量的幅度(Magnitude)提取出来分析。这个幅度就是误差向量幅度,英文名称为Error Vector Magnitude,简称EVM。
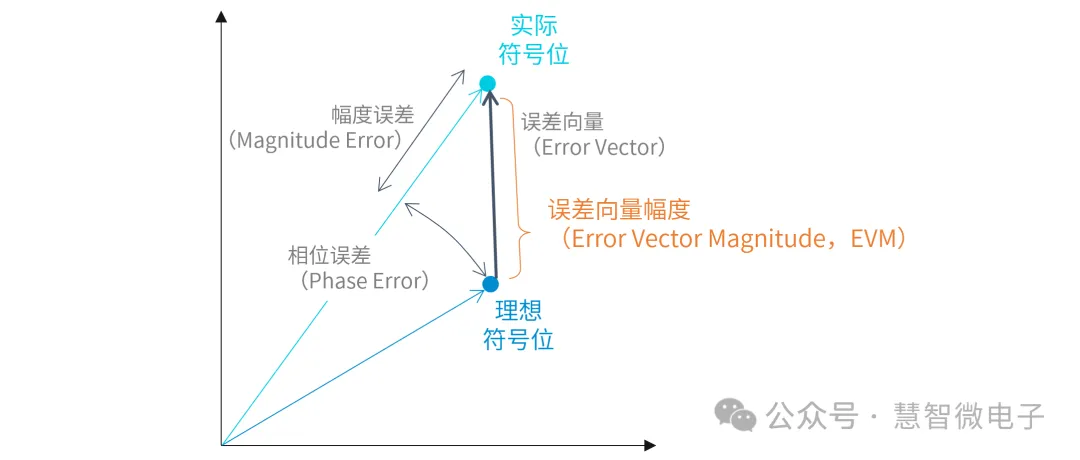
图:EVM的定义
需要注意的是,EVM是“误差向量幅度(Error Vector Magnitude)”,和前述的幅度误差(Magnitude Error)虽然名称中有两个英文单词一样,但却不是一回事。幅度误差只反应两者幅度之间的差别,而EVM反应的是误差向量的幅值。
EVM的计算
在对EVM进行定性了解之后,就可以对EVM进行计算。在计算中,有几个细节需要注意。了解了这些细节,才能对EVM指标有清晰de地了解。这些细节包含:
1. 选峰值还是选均值?EVM中的参考向量选择
2. “%”和“dB”:EVM的两种单位
3. 不同调制的EVM需求计算
4. 器件级连的影响:链路中的EVM
选峰值还是选均值?EVM中的参考向量选择
虽然在前述定义中,EVM是一个反应误差向量幅度的“绝对值”,但在实际使用中,误差向量幅度和有用信号幅度之间的“比值”比误差向量幅度的绝对值更为有意义。所以在使用应用中,EVM经常会做归一化使用。
EVM的归一化有两种方式,一种是对星座图中的最大信号做归一,另外一种是对信号的均方值(RMS)做归一。两种归一化时,所参考的信号如下图所求。
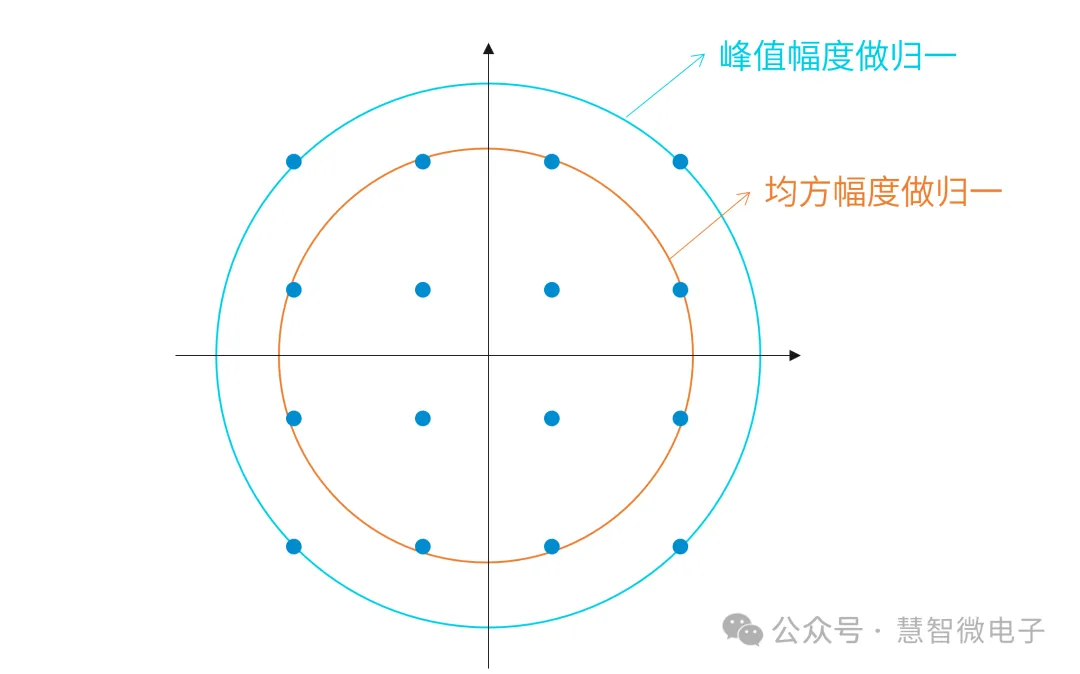
图:EVM归一幅度的两种参考方式
对于EVM计算来说,以上两种选择方式均可,但需要在计算时明确做好约定。例如在Wi-Fi7协议中,就会明确约定归一化选择的功率为星座的“平均”功率,而非最大功率。
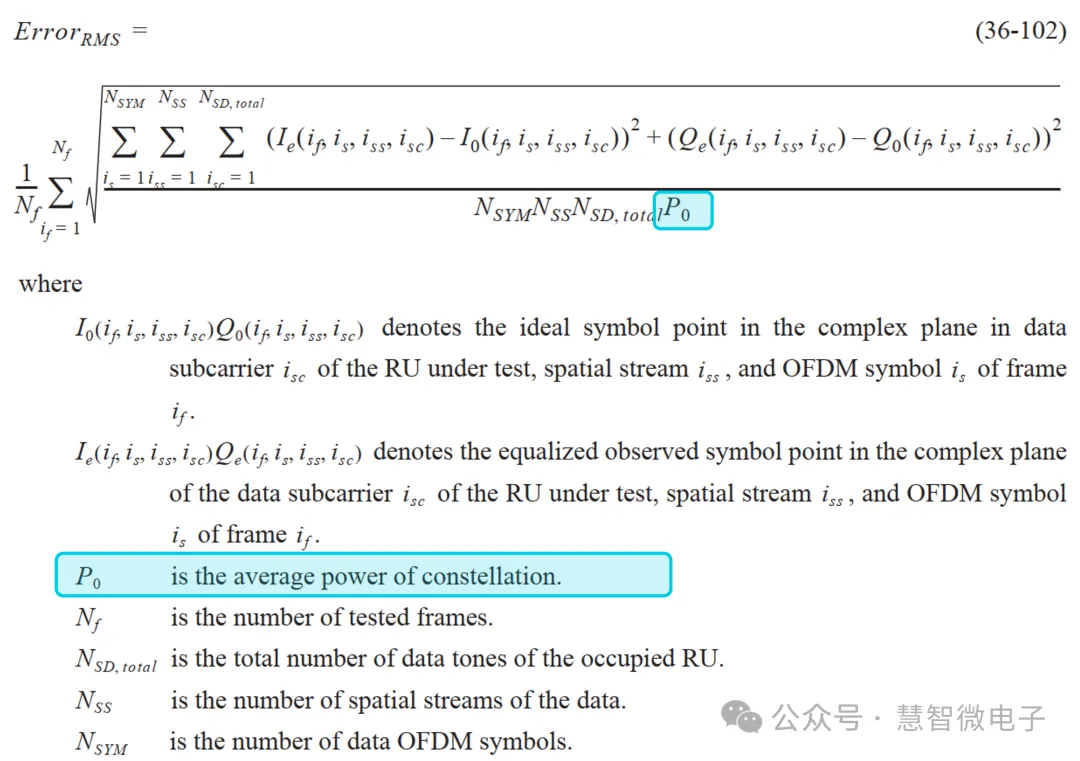
图:Wi-Fi7协议中EVM计算的定义
“%”和“dB”:EVM的两种单位
将EVM信号和实际信号进行比较,就得到EVM的值。归一化后的EVM值为一个百分比。如下图所示。

图:归一化后的EVM,用百分数表示
在射频的计算中,为了方便计算,方便地进行数字的观察处理,经常会用dB为单位来表示倍数或者比例关系。比如对于功率来说,说3dB代表两倍,10dB代表10倍,30dB代表1000倍等。这一方法同样可以在EVM的表征中使用。EVM的dB和倍数之间的转换关系如下所示。
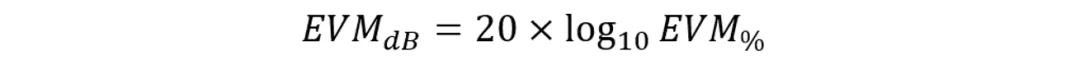
需要说明的是,EVM的%计算时,所使用的是信号“幅度”之间的比值,而非功率。所以在进行dB的转换时,需要用到的是20*Log来转换,而不是10*Log。在转换时需要特别注意。
采用dB表示之后的EVM如下图所示。
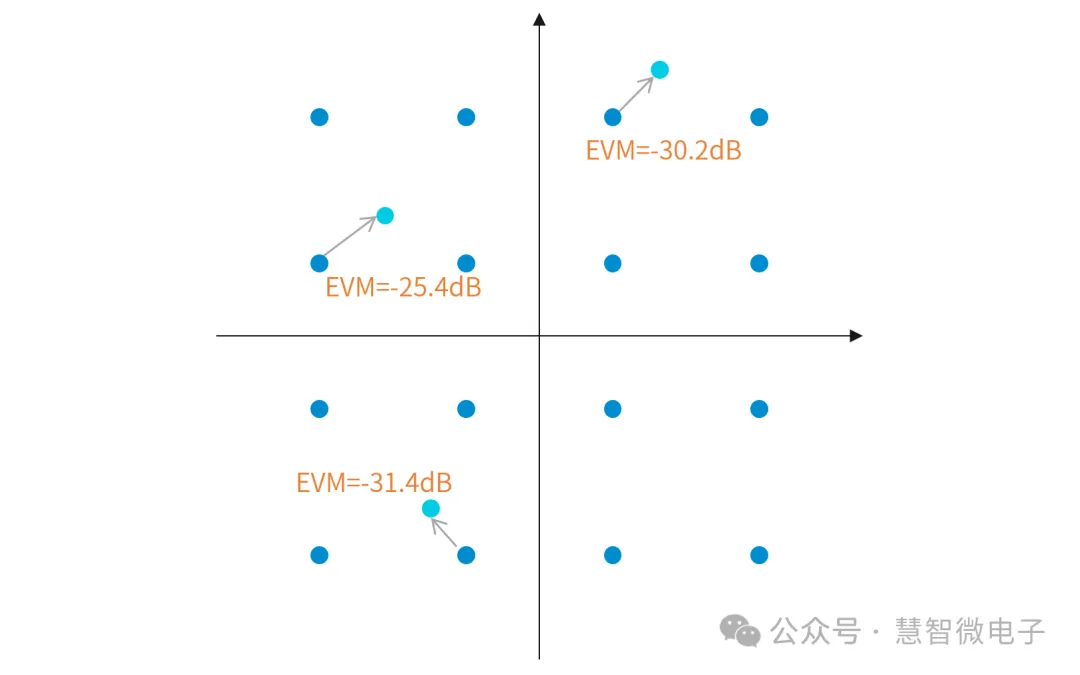
图:采用dB表示的EVM
在不同使用中,为了使用方便,EVM的表征经常会在%和dB两种表示之间切换。为方便使用和转换,整理二者对应关系如下表所示。
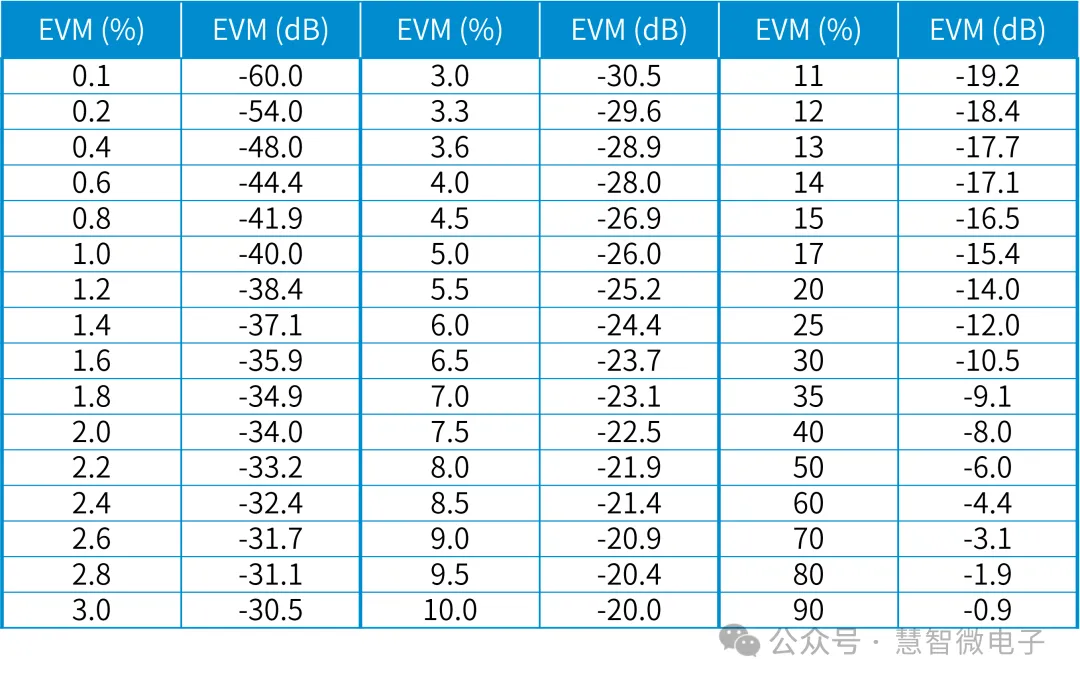
图:采用%和dB表示的EVM相互转换关系表
不同调制的EVM需求计算
了解了EVM的计算方法,我们就可以尝试对不同调制的EVM需求进行计算。以下以64QAM为例,讨论计算过程。
对于64QAM信号,若以符号与符号之间的间隔为定为a,则如果一个符号偏离自己位置0.5a时,将会发生信号的误码。所以极限的EVM绝对值为0.5a。同时,计算64QAM信号的幅度均方值,可得其均方值为3.24a。此时计算64QAM的EVM为:0.5a/3.24a=15.4%,转换为dB表示为-16.2dB。
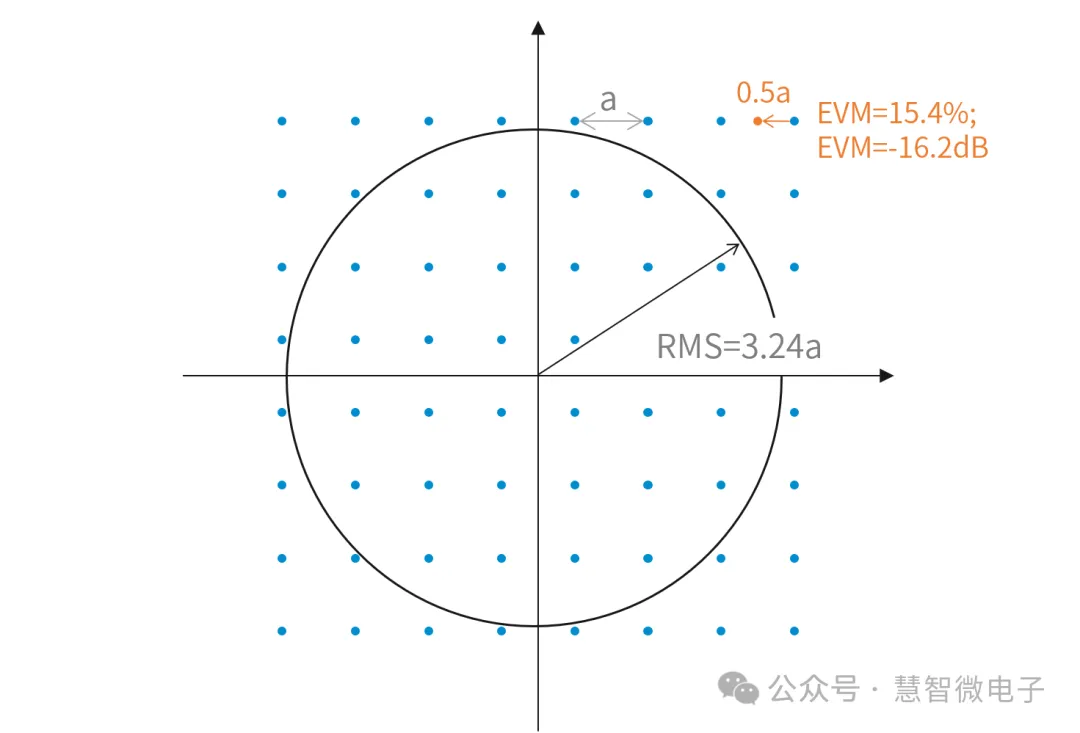
图:64QAM的EVM计算
同理,可以计算256QAM、1024QAM以及4096QAM下的EVM需求,计算结果如下表所示。
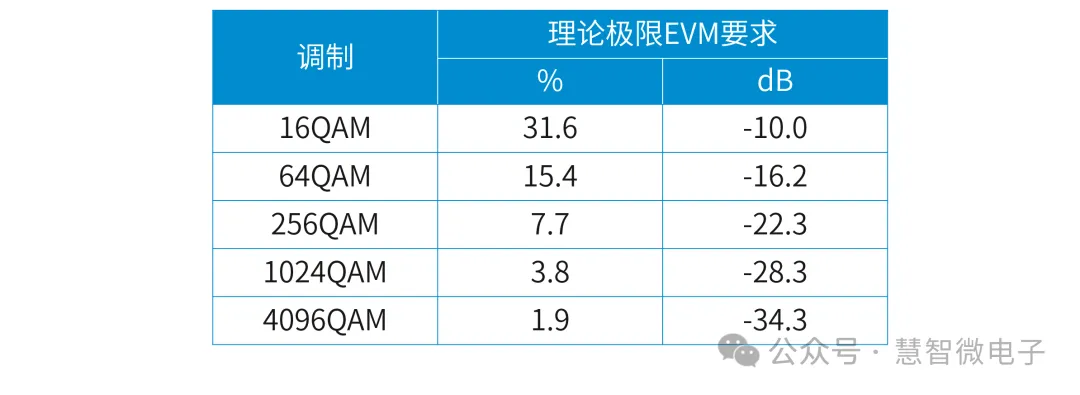
图:不同调制下的EVM极限需求计算
通过上表可以看到,对于越高阶的信号,其对EVM的要求也就越高。在理解上也相对直观:高阶调制下各符号在星座图上的位置也更加靠近,就需要各符号更紧密的围绕在理想符号周围,来确保信号不出现误码。
器件级连的影响:链路中的EVM
在射频发射及接收链路中,不同器件的非理想特性都会对EVM产生影响。对于多级链路,EVM影响可以由以下公式计算:
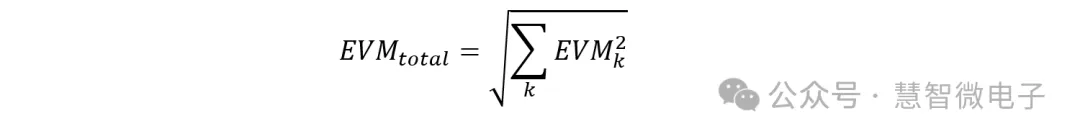
其中k表示不同的EVM来源序号。
采用以上公式时需要注意,以上要求计算各链路EVM的影响之间互不相关。另外,各EVM单位均为%。如果EVM已经用dB表示,需要先将dB转为%,再进行计算。
在实际电路中,电路的非理想影响还可能表现在交调、相位误差、LO泄露等多个方面,也有专门论文讨论和分析各种非理想特性与EVM的对应关系。有需要可以下载相应的论文来参考 [7]。
一些论文也对EVM的来源进行了分析和总结,比如在文章[3]中,在Wi-Fi7的射频收发机芯片设计中,发射链路的EVM中的48%是由IMD所贡献,20%由相位噪声贡献,32由带内噪声贡献;在接收链路中,60%由热噪声贡献,30%由相位噪声贡献,10%来自于其他。
另外,在观察上一部分对EVM的理想计算,以及系统协议对发射EVM的要求,就会发现二者有明显的差别。比如对于4096QAM信号,理论计算1.9%(-34.3dB)的EVM就可以完成传输,但Wi-Fi7协议中却要求达到1.3%(-38dB)。
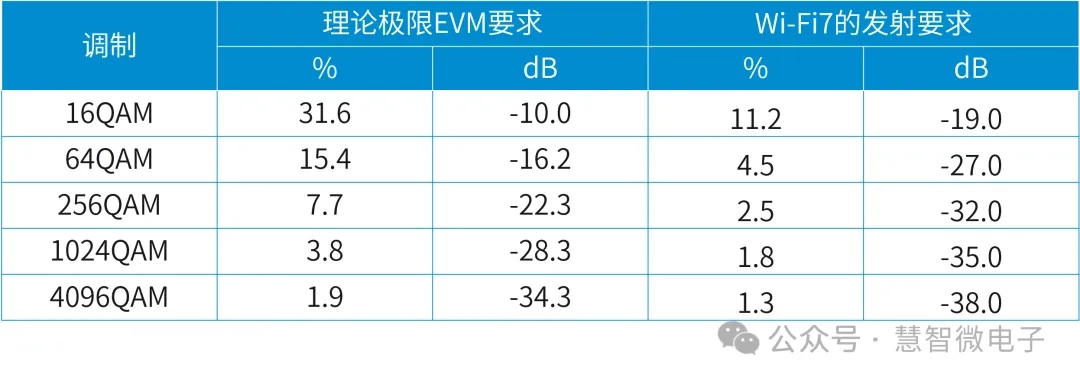
图:EVM的理论要求及Wi-Fi7协议中的发射要求
二者存在区别的原因是还要考虑接收通路的解调对EVM的恶化。并且保持一定的余量来保证信号的误码率不受影响。
影响系统EVM的因素
EVM的定义和计算更多是从系统综合表现维度来看,是多重影响下的表现结果。在一个通信系统中,可能会对EVM产生影响的原因比较多,常见的有以下影响:幅度影响、相位影响、IQ不平衡影响、其他影响。
幅度影响
通过星座可以看到,当信号幅度发生变化时,将影响信号与理想信号之间的偏移,进而影响EVM。
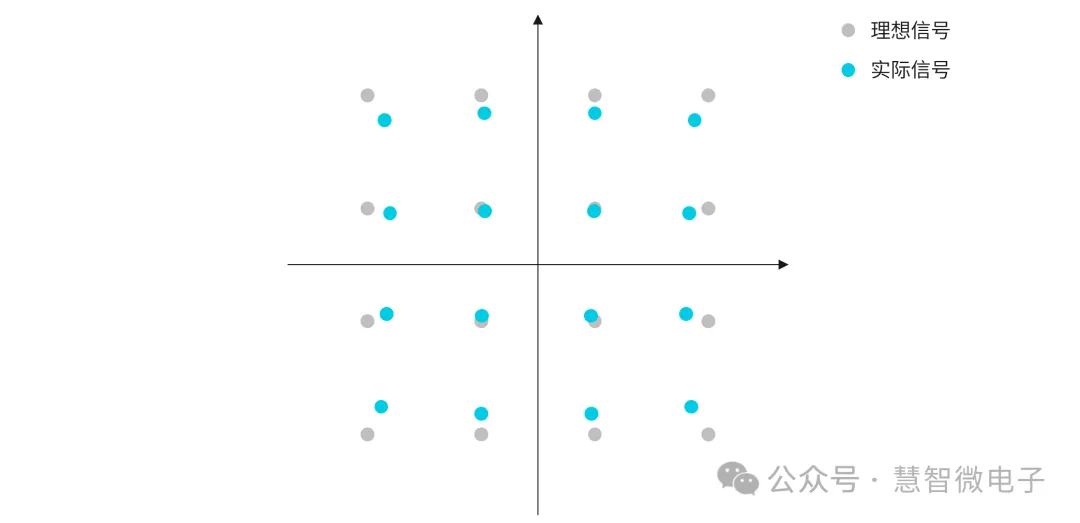
图:幅度对EVM的影响
射频通信中,功率放大器(PA)作为发射链路的重要单元,若其幅度出现非理想特性,将会对系统EVM的影响。
PA的幅度响应曲线一般用AM-AM(Amplitude Modulation -Amplitude Modulation,幅度-幅度调制)来表示。AM-AM曲线的横轴为输出功率,纵轴为幅度的放大量,也就是增益。对于放大器,其AM-AM曲线一般形状如下图所示。
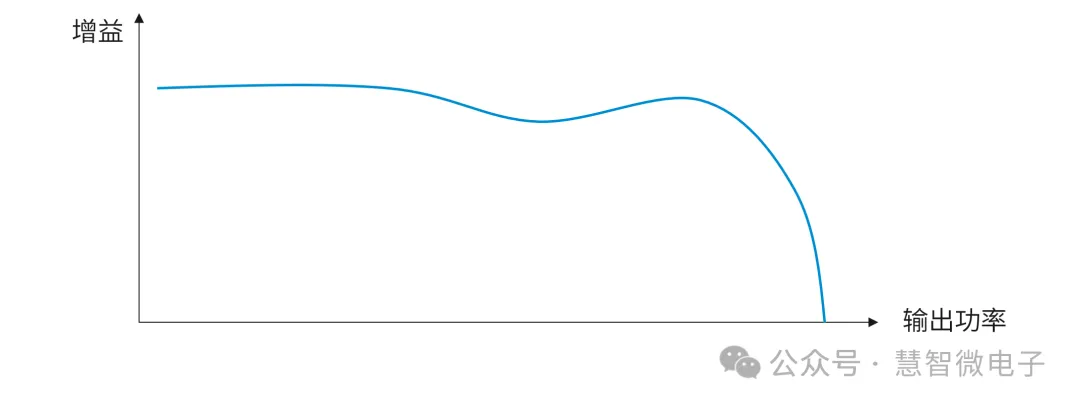
图:放大器的AM-AM曲线
在以上曲线中,放大器有一定的增益,并且由于非理想效应,或者所选用放大器的特殊架构原因,其增益会在一定范围内发生变化。另外,在达到一定输出功率时,由于放大器会出现功率饱和,无法无限制的输出功率,所以对应增益曲线也会下折下来。
由于调制信号不同符号位的幅度不同,所以就有可能对应到放大器不同的输入信号幅度上。如果这两个符号位对应的放大器的增益差别过大,就造成经过放大器之后幅度相对关系发生变化。也就是EVM性能发生了恶化。
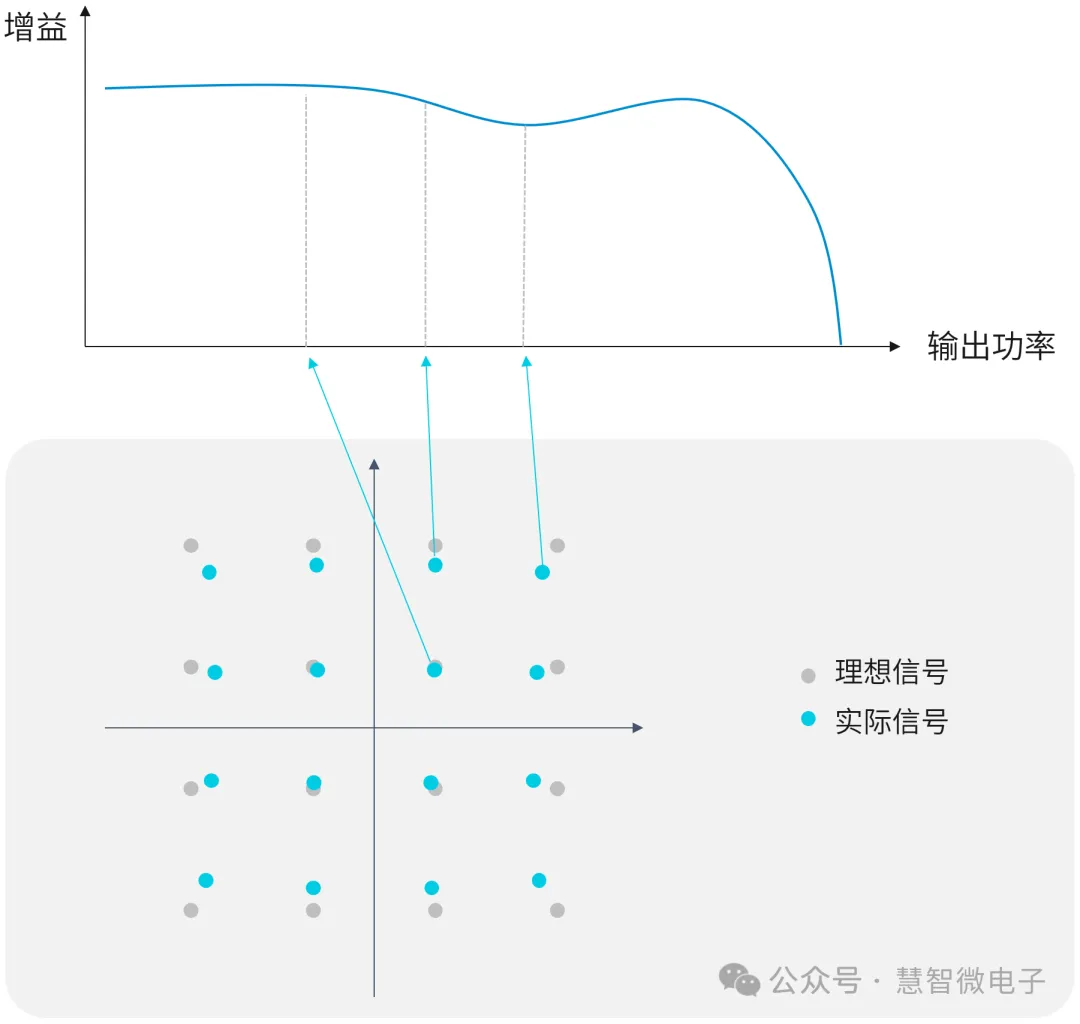
图:放大器的AM-AM特性对EVM的恶化
正是因为这个原因,越先进的通信制式对PA的AM-AM特性要求越高,越需要足够平缓的AM-AM曲线。以64QAM到4096QAM的演进为例,对PA的AM-AM曲线要求可表示为如下关系。
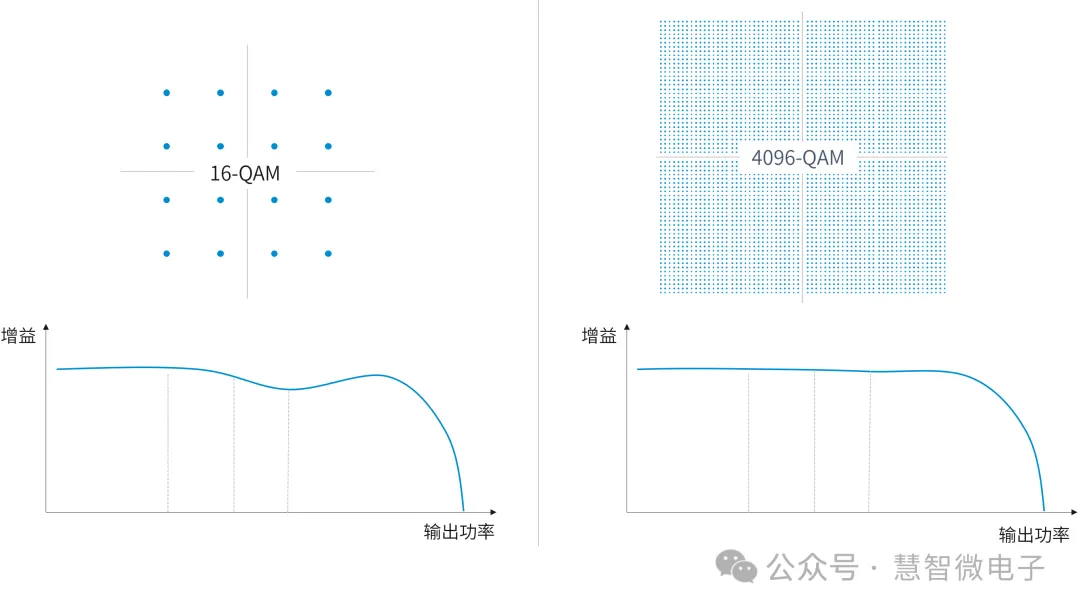
图:不同调制对PA AM-AM曲线的要求
相位影响
在整个通信系统中,经过非理想器件时,产生变化的不止是信号的幅度,还有信号的相位。同样以功率放大器来说,其不同功率下相位的变化一般用AM-PM(Amplitude Modulation-Phase Modulation,幅度-相位调制)曲线来表示。和AM-AM曲线相同,AM-PM曲线变化的越剧烈,其对EVM的影响就会越明显。
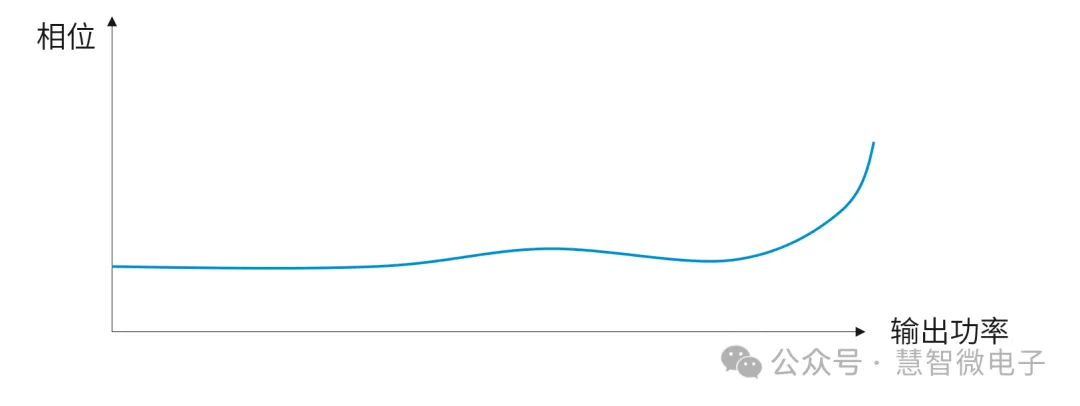
图:AM-PM曲线
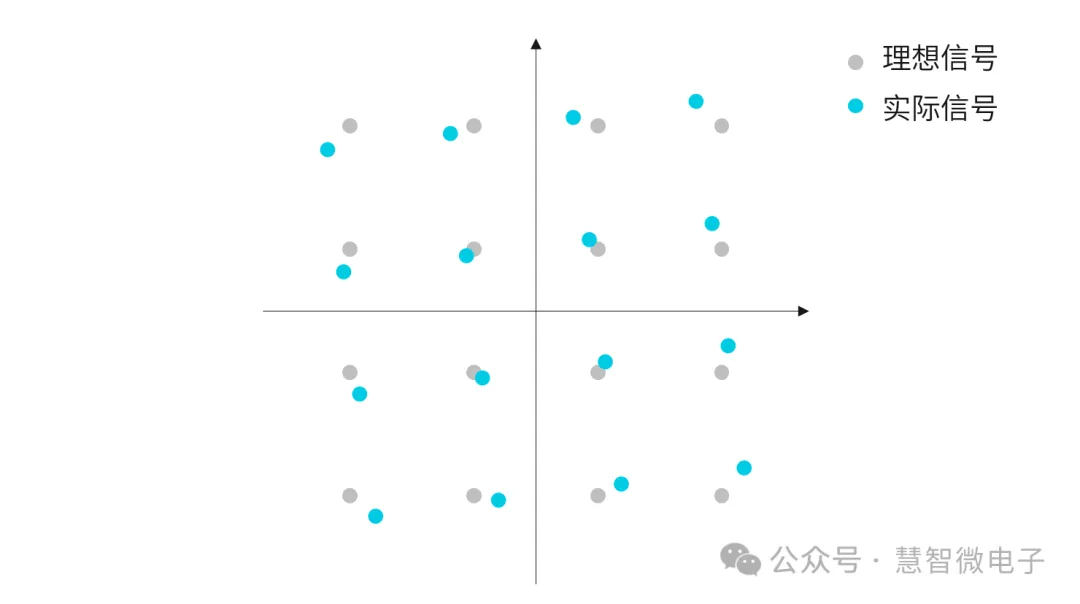
图:相位对EVM造成的影响
IQ不平衡影响
在通信系统的构建中,特定向量的产生一般通过I路和Q路两个信号的加合来形成。合成中,均是假定I和Q路完全对称。但在实际电路中,电路之间可能存在误差。若I和Q路出现不平衡,则将使合成的信号位置产生误差。例如,假定I路信号的幅度产生90%的偏移时,产生的EVM如下图所示。
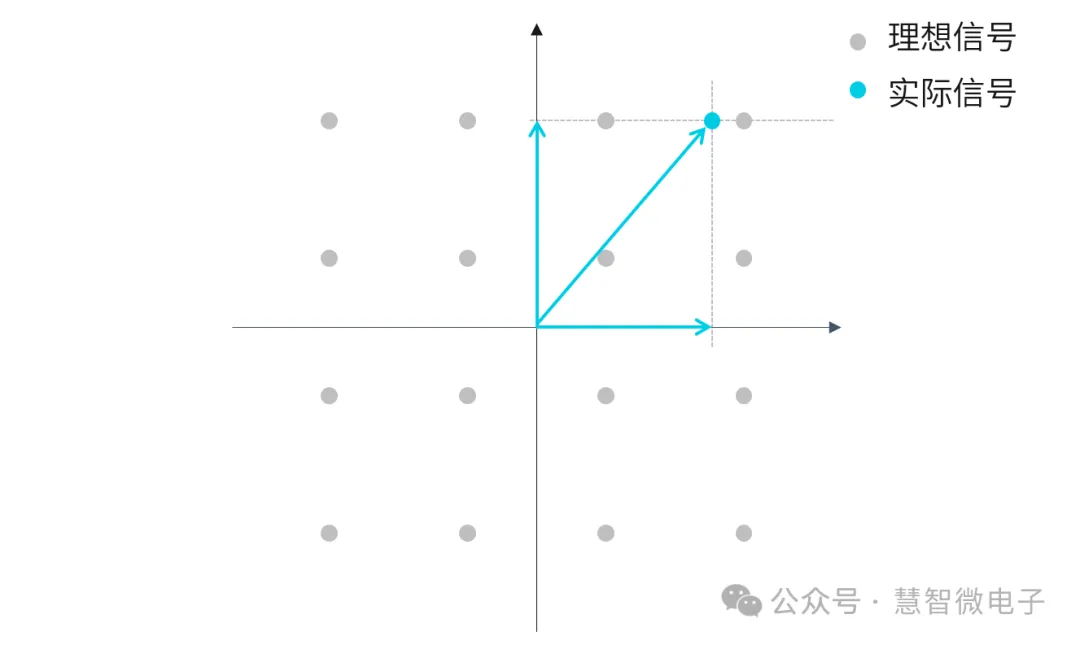
图:IQ不平衡引起的EVM
其他影响
除了上述幅度影响、相位影响以及IQ不平衡影响,还有其他多种因素会对EVM产生影响。比如:相位噪声、LO泄露、信号交调、其他频率干扰等。影响EVM的因素可能是多方面的,在实际分析中,需要根据实际情况加以分析。
EVM的应用
了解了EVM的物理意义、产生机理之后,就可以在应用中使用EVM来指导电路设计,或者是问题解决。
在应用中,EVM还可以和其他参数结合,以得到更多的信息。常见的和EVM结合分析的参数主要有:
1. EVM和功率的结合:分析器件最大功率
2. EVM和时间的结合:分析器件时域表现
3. EVM和频率的结合:分析系统干扰频率
EVM和功率的结合:分析器件最大功率
EVM和功率结合的分析方法经常应用在发射通路器件的评估中。
发射通路的重要器件是功率放大器(PA),在PA分析中,经常会用到EVM和输出功率结合的方式,来观测PA的最大输出能力。
下图为慧智微某款Wi-Fi7 FEM的EVM与功率曲线。可以看到,在整体应用区间,慧智微Wi-Fi7 FEM有着良好的EVM特性。随着功率的升高,在达到标称功率之后,由于器件的饱和,EVM曲线开始恶化上升。当EVM曲线达到指标临界时对应的功率点,就为此FEM能工作的最大功率。如下图慧智微Wi-Fi7 FEM产品,在维持-46~-47dB EVM性能时,可以达到17dBm输出功率。
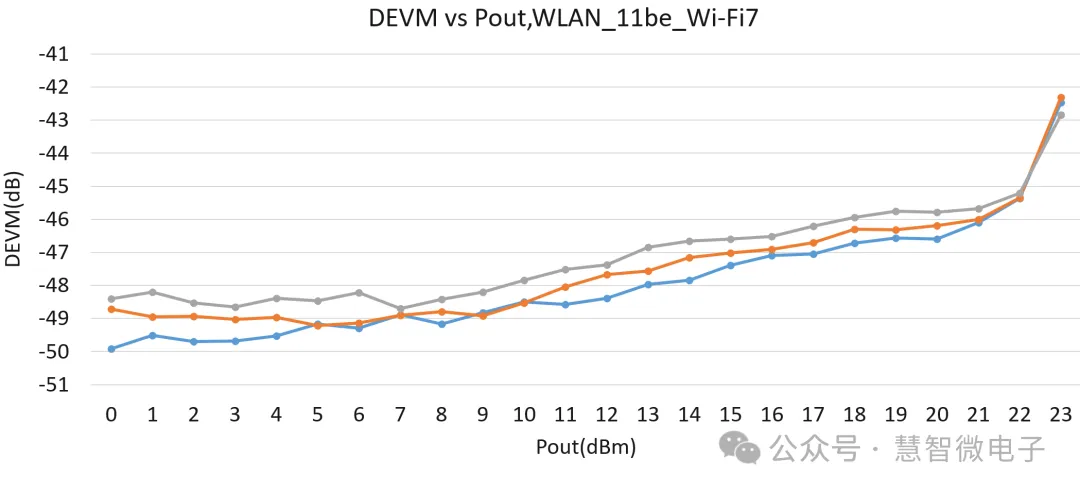
图:慧智微Wi-Fi7 FEM EVM曲线
EVM和功率结合的分析方法也可以用来分析射频收发机(Transceiver)的性能。下图为典型射频收发机输出表现能力图示,收发机EVM能力随功率变化呈“浴盆曲线”形状。在低工作功率水平下,EVM性能主要由系统的噪声性能决定。在高工作功率水平下,EVM主要由系统的非线性决定。系统的最低EVM水平(EVM Floor)通常根据所有误差源(包括相位噪声)的组合来决定。
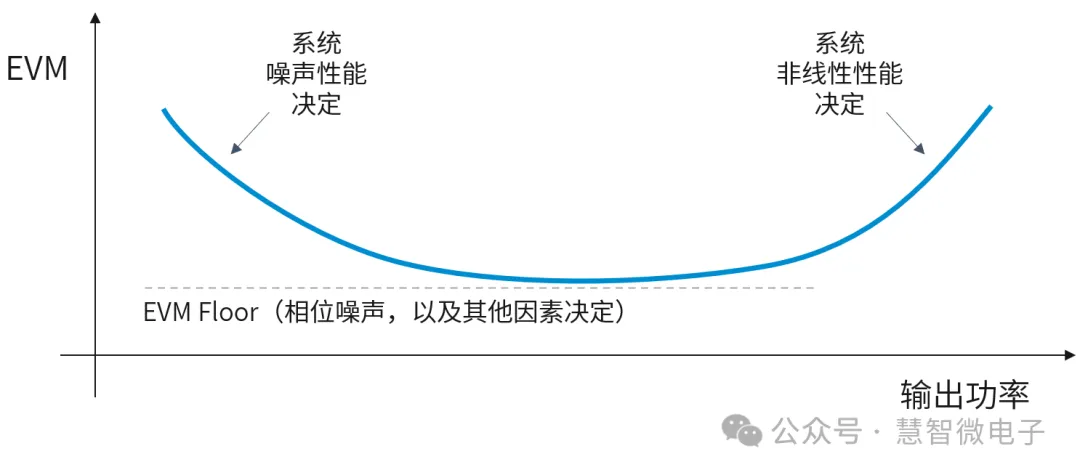
图:典型射频收发机输出EVM能力的“浴盆曲线”
为了适配更大的功率范围,射频收发机会采用不用的功率模式进行设计,以使工作功率的EVM值达到最优状态。下图为某ADI收发机多档位下EVM与功率的对应曲线。
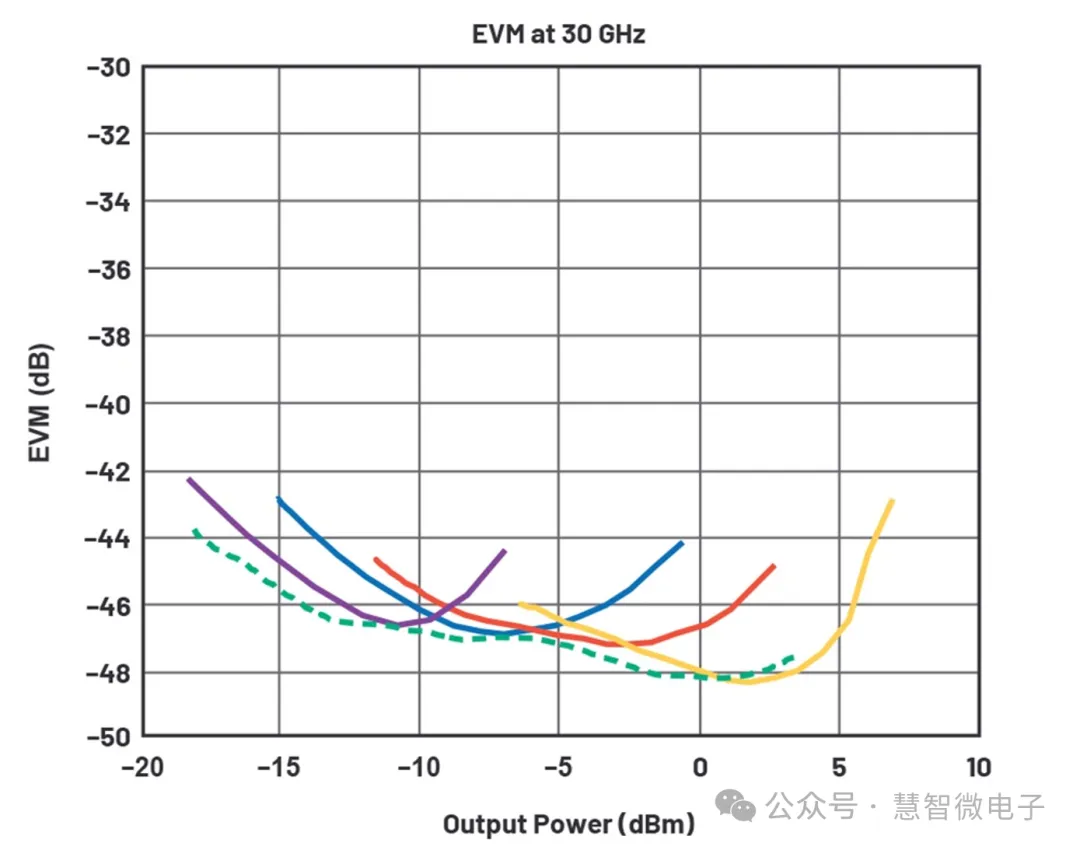
图:ADI收发机EVM随功率变化特性
EVM和时间的结合:分析器件时域表现
通过EVM与时间的结合,可以看出器件特性随时间的变化。
EVM随时间的变化曲线在Wi-Fi系统中尤其重要。Wi-Fi是一个TDD系统,在Wi-Fi信号传输过程中,发射和接收信号在快速进行切换。但由于PA的稳态建立需要一定的时间,在这个稳定时间到来之前,不希望系统传输有用信息。而Wi-Fi系统的帧结构复杂 ,在头部的Preamble、header帧中带有同步符号、样本信号、传输参数等信息,这就需要PA快速建立,用来响应帧头部的重要信息。

图:Wi-Fi的帧结构信息
但对于PA电路,PA的偏置电流随TDD脉冲不断打开和关闭,PA电流的建立本身需要一段时间来响应。另外,电流稳态建立之前,PA的温度也随着电流的变化而变化,造成PA本身的增益、相位特性均在变化。因为Wi-Fi系统的EVM参考信息在Preamble中进行传输,PA在Preamble及后续数据传输中状态的不一致,造成系统EVM的恶化。所以在Wi-Fi系统中,除了查看静态EVM之外,还会重点查看DEVM(Dynamic EVM,动态EVM)。而器件随时间变化的特性,也是DEVM恶化的来源。
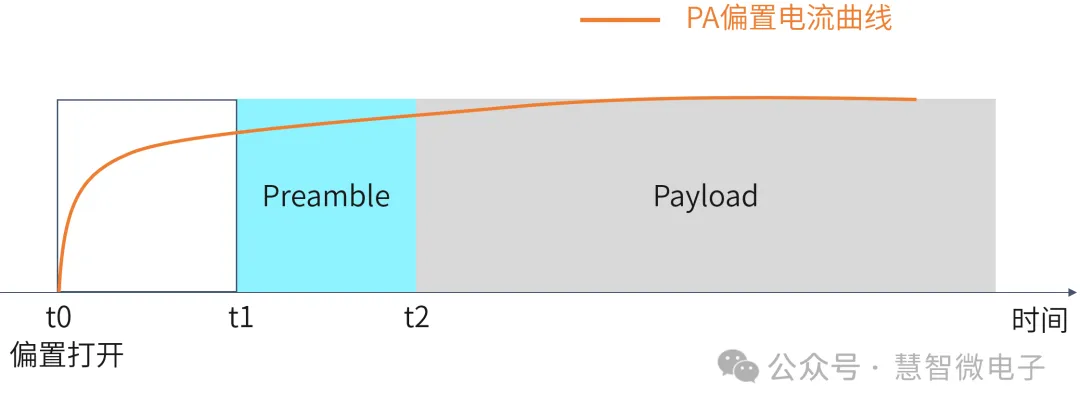
图:PA特性随时间的变化,造成系统DEVM恶化
下图为文献中,实际测试中PA输出功率随时间变化的曲线,及其对EVM的影响。可以看到PA输出功率随时间的变化,以及对DEVM产生的影响。
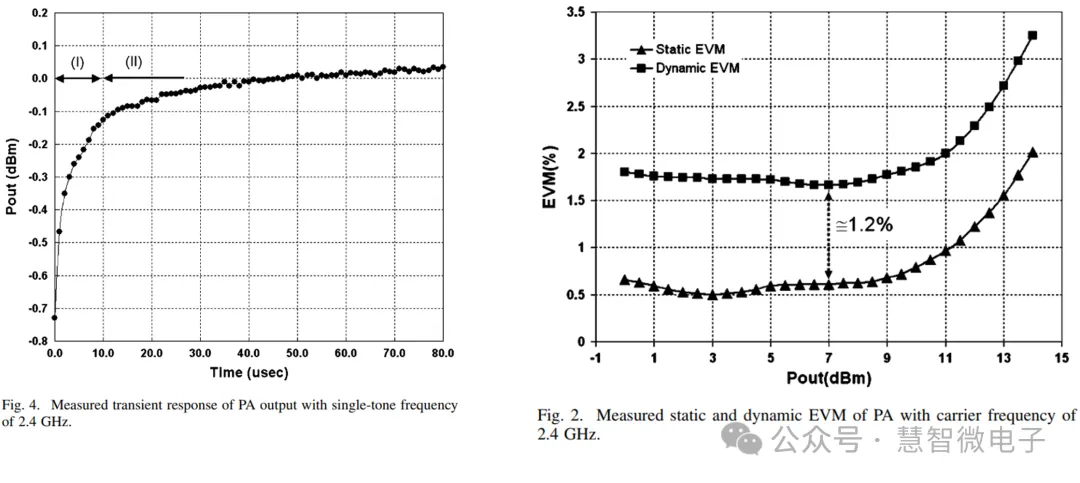
图:实际测试中PA输出功率随时间变化的曲线,及其对EVM的影响
为了改善以上问题,一般会加入补偿电路。补偿电路的存在,可以提供一个瞬态电流补偿,将PA的偏置电流瞬间拉到所需要的静态值,然后再慢慢衰减下来,确保PA的总偏置电流一直维持固定值。从而保证EVM不随时间变化而变化。
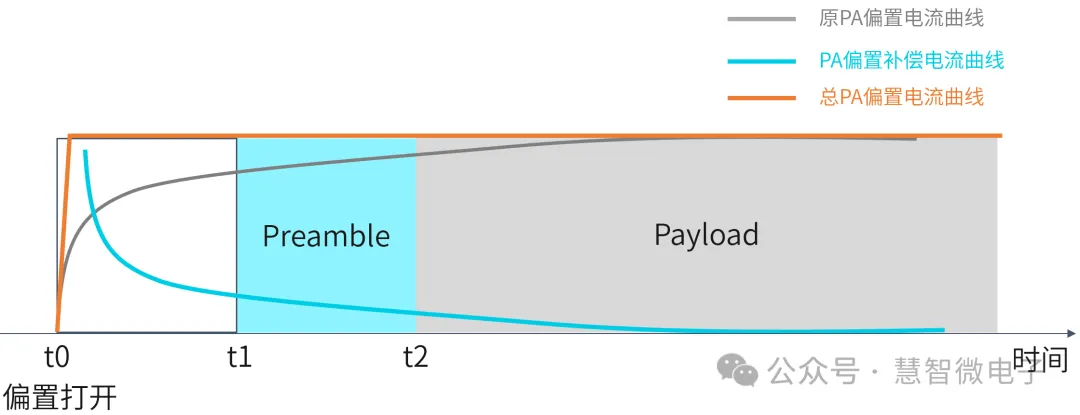
图:DEVM的改善技术
EVM与频率的结合:分析系统干扰频率
不止可以从时域角度来观察EVM,将时域EVM信号进行傅立叶变换,转化到频域之后,同样可以看到众多信息。
比如当EVM恶化时,在频域对EVM进行分析,可以看到EVM恶化的频率点,从而有助于找到干扰来源,对系统进行改善。
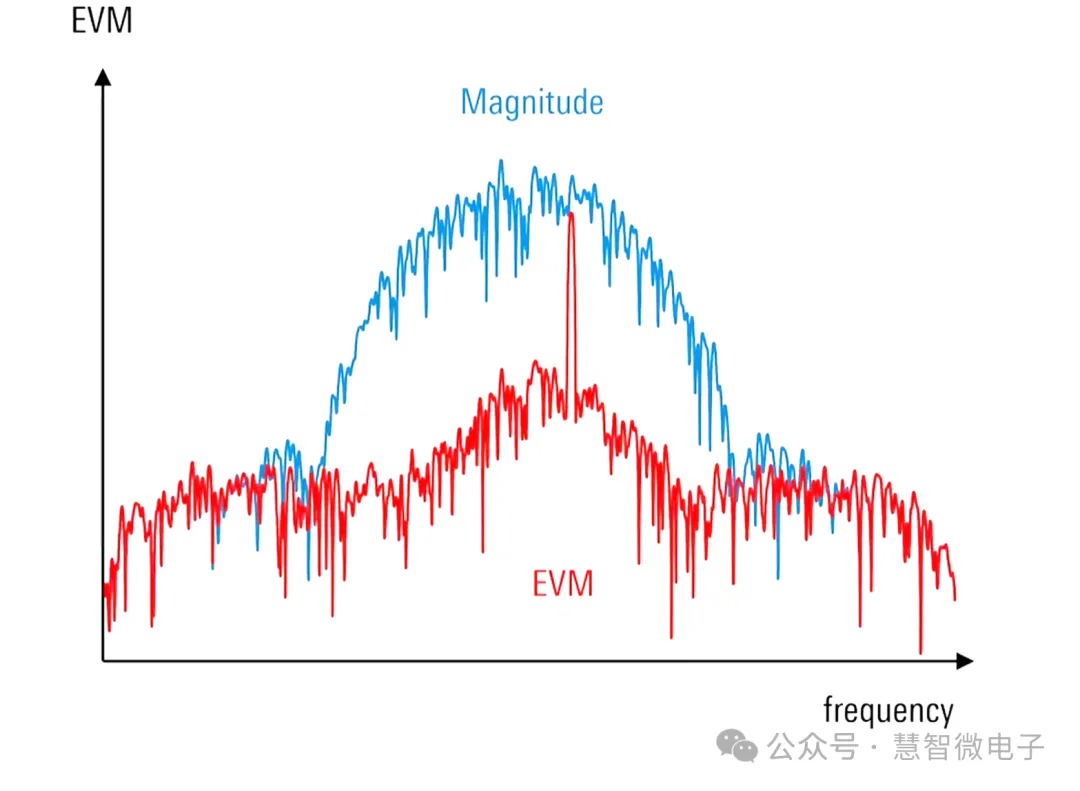
图:EVM对频率做图观测干扰信号频率
总结
EVM是现代数字通信中的重要指标之一,深入理解EVM指标对于电路设计、系统设计,以及问题解决有重要帮助。
本篇尝试从EVM的起源背景、精确定义、计算方法以及它对通信系统性能的具体影响等方面,分析EVM指标的理论基础、实际应用中的挑战与系统优化和故障诊断。










